Forma arbitrarioak dirudite, baina kaosak ere badauka bere ordena. Matematikaren bidez azaldu daiteke iratze baten egitura eta haren hosto biribilduak; geometria bat daukate kostaldearen ertzen anabasak, gorputzeko odol hodien eta nerbioen matazak, biriketako adarkatzeek. Ez dira lerroak, ez karratuak, ez kurbak, ez borobilak. Beste zerbait dira. Benoit Mandelbrot matematikariak berba iradokitzaile batekin izendatu zituen orain dela 50 urte: fraktalak. Latinezko fractus hitzetik hartu zuen kontzeptua: hots, apurtua, hautsia. Mugarri bat ezarri zuen hala, eta bidea eman zion matematikaren eremu zabal eta oparo bati: gaur egun, askotariko arloei egiten die ekarpena geometria fraktalak.
Mandelbrotek izendatu egin zituen, eta, dibulgazio lan nabarmen bati esker, publiko orokorrarengana helarazi zituen fraktalak. Baina lehenagotik ziren matematikarien buruhauste. XIX. mendearen bukaeran eta XX. mendearen hasieran jada bazeuden matematikaren moldeekin bat etortzen ez ziren zenbait gauza, EHUko Geometria irakasle Raul Ibañezek azaldu duenez. «Hainbat motatako propietate matematikoak aztertzen ari ziren, eta zenbait paradoxa zeuden. Hitz soiletan esatearren, ordura arteko matematika oso leuna zen; geometrian, kurbak, azalerak eta abar zeuden, baina gauza batzuetan ez zegoen leuntasunik, zimurtasuna baizik». Garai hartako matematikari handi askok jorratu zuten bide zimurtsu hori —hala nola Bernhard Riemannek, David Hilbertek eta Felix Hausdorffek—, eta intuizioari kontraesan egiten zioten ezaugarri geometriko eta analitikoak zituzten objektuak sortu zituzten: Giuseppe Peanoren kurba —karratu bat betetzeko gai dena—, Waclaw Sierpinskiren triangelua, Helge von Kochen elur maluta eta Georg Cantorren multzoa dira orduko ekarpenetako zenbait.
Baina zer dira, zehazki, fraktalak? «Konplexua da definizio bat ematea», onartu du Ibañezek. Izan ere, azalpenik gabeko problema asko batu zituzten zaku horretan. Hiru propietate dituzte, baina fraktal guztiek ez dituzte ezaugarriok betetzen. Eta, gainera, ez dira gauza bera fraktal matematikoak —Peanoren kurba eta enparauak— eta naturan topa daitezkeenak: lehenak objektu «idealak» dira; bigarrenak, berriz, hurbilpenak.

Fraktalak autoantzekoak dira. Hau da, egitura bera errepikatu egiten da eskala ezberdinetan. «Objektu fraktal bat hartuz gero eta zati bat handituz gero, originalaren egitura berdin-berdina izango du. Eta horrek arreta pizten du, esan dezakegu eta objektua bere buruaren kopiekin osatuta dagoela, infinitura arte». Romanesko azalorean argi ikus daiteke errepikapen hori; barazki hura erabili ohi da, hain zuzen, naturaren izaera fraktala erakusteko: azalorearen loreek kono itxura dute, eta forma bera errepikatuz doa loreen barruan, gero eta tamaina txikiagoan. Fenomeno bera antzeman daiteke beste barazki batzuetan, hostoetan, arboletan... «Halakoetan, autoantzekotasuna ez da zehatz-zehatza», egin du ñabardura matematikariak.
Horrez gain, fraktalek ezohiko dimentsioak dituzte. Zenbaki naturalekin adieraz daitezke geometria klasikoko figuren dimentsioak: kurbak bakarra dauka, azalera batek bi dauzka, eta esfera batek, hiru. Baina, fraktalen kasuan, erdibideko zenbakiak dira: hala, Cantorren multzoak 0,6319ko dimentsioa du, eta Kochen kurbak, berriz, 1,2618koa. «Dimentsio fraktal horrek zerikusi handia dauka, modu sinple batean esateko, objektuaren zimurtasunarekin: hau da, ez da objektu lau bat». Kostaren paradoxan agerikoa da hori. «Argazki batean neurtzen badugu zer luzera duen kosta batek, datu bat lortuko dugu, baina, bertara bagoaz eta oinez neurtzen badugu, luzera handiagoa emango liguke; eta are handiagoa inurri batek neurtuko balu». Eskala zenbat eta gehiago murriztu, orduan eta handiagoa izango da perimetroa, infinitura heltzeraino, Mandelbrotek azaldu zuenez. «Paradoxikoa da, uste baitugu halako luzera batek finitua izan beharko lukeela».
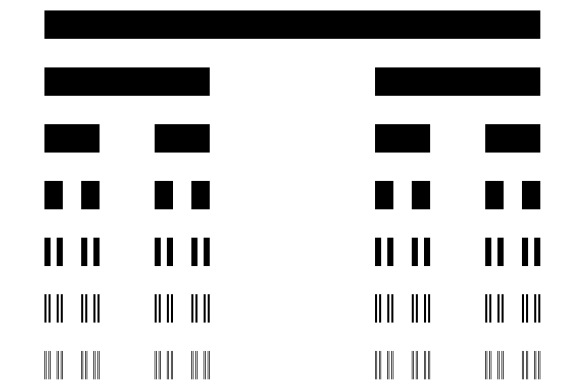
Hirugarren ezaugarriak aurreko biak osatzen ditu, Ibañezen esanetan: ikuspuntu matematikotik, prozesu iteratibo infinitu gisa deskribatu ohi dira objektu fraktalak. Hau da, prozesu jakin bat aplikatzen da, horren emaitzari prozesu bera aplikatzen zaio, eta beste horrenbeste kasuan-kasuan ateratzen diren emaitzei. Cantorren multzoa erabili ohi du Ibañezek segida hori azaltzeko: 1 luzerako lerro bat hiru zatitan banatzen da, eta erdiko segmentua ezabatzen da, muturretako biak baino ez utzita; segmentu horietako bakoitza (1/3) hiru zatitan banatzen da ostera, eta erdikoa kentzen da; berdin egiten da geratu diren zatiekin (1/9), eta horrela infinitu bider. Propietate horri dagokionez ere, ez dute berdin jokatzen fraktal matematikoek eta naturalek: matematikariak zehaztu duenez, naturako fraktalek lauzpabost iterazio izan ohi dituzte, gehienez.
Konplexutasuna lantzeko
Fraktalen aurkikuntzak geometriaren aukerak zabaldu zituen, nolabait. Aurretik, geometria klasikoaren objektuak erabiltzen ziren modelo matematikoak sortzeko, baina mugak zituzten. Mandelbroten esaldi ezagun batek laburbiltzen du arazoaren muina: «Hodeiak ez dira esferak, mendiak ez dira konoak, kostak ez dira zirkularrak eta tximista ez doa lerro zuzenean». Eta ondorioa bota du Ibañezek, jarraian: «Matematikoki zerbait modelizatu nahi badugu, errealitatearen konplexutasunera egokituko diren objektuak behar ditugu». Alegia, fraktalak.
«Argazki batean neurtzen badugu zer luzera duen kosta batek, datu bat lortuko dugu, baina, bertara bagoaz eta oinez neurtzen badugu, luzera handiagoa emango liguke»
RAUL IBAÑEZ EHUko Geometria irakaslea
Horrenbestez, ia edozein eremutan aplikatzen dira, matematikariak zerrendatu duenez. Konputazioan, irudiak konprimatzeko teknika batzuk fraktaletan oinarritzen dira; infografietan barra-barra baliatzen dira, pelikuletan aspalditik ageri dira, eta publizitatean oso eraginkorrak dira paisaia, objektu edo testura konplexuak diseinatzeko; medikuntzan, osteoporosia, odol hodiak, birikak, garuna eta egitura bihurgunetsuak dituzten beste organo eta sistema batzuk modelizatzeko erabiltzen dituzte; biologian, ehunen hazkundearen, zelulen organizazioaren eta populazioen bilakaeraren berri ematen dute, eta patroi sismikoak eta harrien higadura aztertzeko tresna bikainak dira geologian. Eta habia egin dute, orobat, ekonomian, telekomunikazioetan, meteorologian, ingeniaritzan eta akustikan, adibidez.
Baita artean ere; analisirako baliatzen dira, baita sorkuntzarako ere. Kasurako, Jackson Pollocken artelanek dimentsio fraktal antzekoa zutela ondorioztatu zuten ikerketa batean. Eta, sorkuntzaren bideari erreparatuta, fraktalak tresna emankorrak dira hainbat artista garaikiderentzat figura eder eta interesgarriak taxutzeko. Bruno Munari italiarrak Peanoren kurba darabil; Mel Bochner pintore estatubatuarrak eta Anton Bakker eskultore herbeheretarrak, berriz, Pitagorasen arbola; eta Veronica Navarro espainiarrak Kochen elur malutaren moldean ebakitzen du papera, eta beste hainbat figura fraktal landu izan ditu, halaber.

«Duela urte batzuk, boladan egon zen arte fraktala», oroitu du matematikariak. Ez da aipatutako artistek lantzen duten gauza bera —ordukoek algoritmoak erabiltzen baitzituzten—, baina erakusten du zer-nolako moldagarritasuna duen geometria mota horrek. «Garai hartan, ordenagailuetan Mandelbroten multzoa eta beste fraktal batzuk erabiltzen ziren, eta, zoom eginda, irudi oso ederrak lortzen ziren. Pintore batek pintura eta pintzela erabiltzen dituen legez, artista haiek algoritmo fraktalak eta kolore algoritmoak erabiltzen zituzten».


